Van Decimaal naar Binair

Inleiding

Een computer bewaart gegevens volgens het binaire stelsel. Het binaire stelsel gebruikt enkel de symbolen 0 (schakelaar uit) en 1 (schakelaar aan) om gegevens voor te stellen. De symbolen 0 en 1 worden aangeduid met de term bit (een samentrekking van de binary digit). In de les Van Decimaal naar Binair ontwikkelen we een programma om een geheel getal uit het decimale stelsel om te zetten naar een binair getal.

Talstelsels

Het decimale stelsel

Het decimale stelsel (ook het tiendelig stelsel genoemd ) is gebaseerd op 10 symbolen (0, 1 ,2,…9). De positie van een bepaald symbool in het getal bepaalt de waarde in het getal. Het getal 324 bestaat uit 3 cijfers waarbij het cijfer 4 (positie 0) verwijst naar de eenheden (4*10⁰=4), 2 verwijst naar de tientallen (positie 1) (2*10¹=20) en 3 naar de honderdtallen (positie 2) (3*10²=300). De positie van het symbool in het getal (0, 1, 2) bepaalt dus de waarde van het symbool als macht van 10.

Het binaire stelsel

Het binaire stelsel gebruikt slechts 2 symbolen (0 en 1). Ook in het binaire stelsel is de positie van een symbool belangrijk om de juiste waarde te bepalen. In het binaire stelsel wordt de positie (0, 1, 2…) gebruikt als macht van het getal 2. De waarde van het binaire getal 101000100 kan dan als volgt worden berekend (van rechts naar links): 0*2⁰ + 0*2¹ + 1*2² +0*2³ + 0*2⁴ + 0*2⁵ + 1*2⁶ + 0*2⁷ + 1*2⁸ = 4 + 64 + 256 = 324.

Van Decimaal naar het Binair: Algoritme

Hoe een decimaal getal omzetten naar een binair getal?

Het omzetten van een decimaal getal naar een binair getal kan gebeuren door herhaalde deling door 2 waarbij de restwaarde van elke deling steeds vooraan het binair getal wordt toegevoegd.

Bewerking	Binair Getal
324 : 2 = 162 rest 0	0
162 : 2 = 81 rest 0	00
81 : 2 = 40 rest 1	100
40 : 2 = 20 rest 0	0100
20 : 2 = 10 rest 0	00100
10 : 2 = 5 rest 0	000100
5 : 2 = 2 rest 1	1000100
2 : 2 = 1 rest 0	01000100
1 : 2 = 0 rest 1	101000100

Variabelen

De benodigde variabelen kunnen gemakkelijk worden afgeleid vanuit bovenstaand voorbeeld. Het origineel getal (het getal 324) willen we bewaren in de variabele OrigineelGetal. Het quotiënt van een deling door 2 wordt opgeslagen in de variabele Quotient (het getal 162 na eerste deling) en de rest wordt bijgehouden in de variabele Rest(het getal 0 na eerste deling). Het binair getal bouwen we dan op in de variabele BinairGetal.

Algoritme

De conversie is volledig uitgevoerd als de variabele Quotient nul wordt. De pseudocode kan nu als volgt worden opgebouwd:

Maak BinairGetal leeg
Input OrigineelGetal
Plaats OrgineelGetal in Quotient
Repeat Until Quotient = 0
   Plaats de restwaarde van Quotient / 2 in de variabele Rest
   Voeg de variabele Rest vooraan toe aan BinairGetal
   Plaats de gehele waarde van Quotient / 2 in Quotient
End Repeat
Output BinairGetal

Van Decimaal naar Binair: Scratch-programma

De omzetting van de pseudocode naar een Scratch-programma levert weinig problemen op:

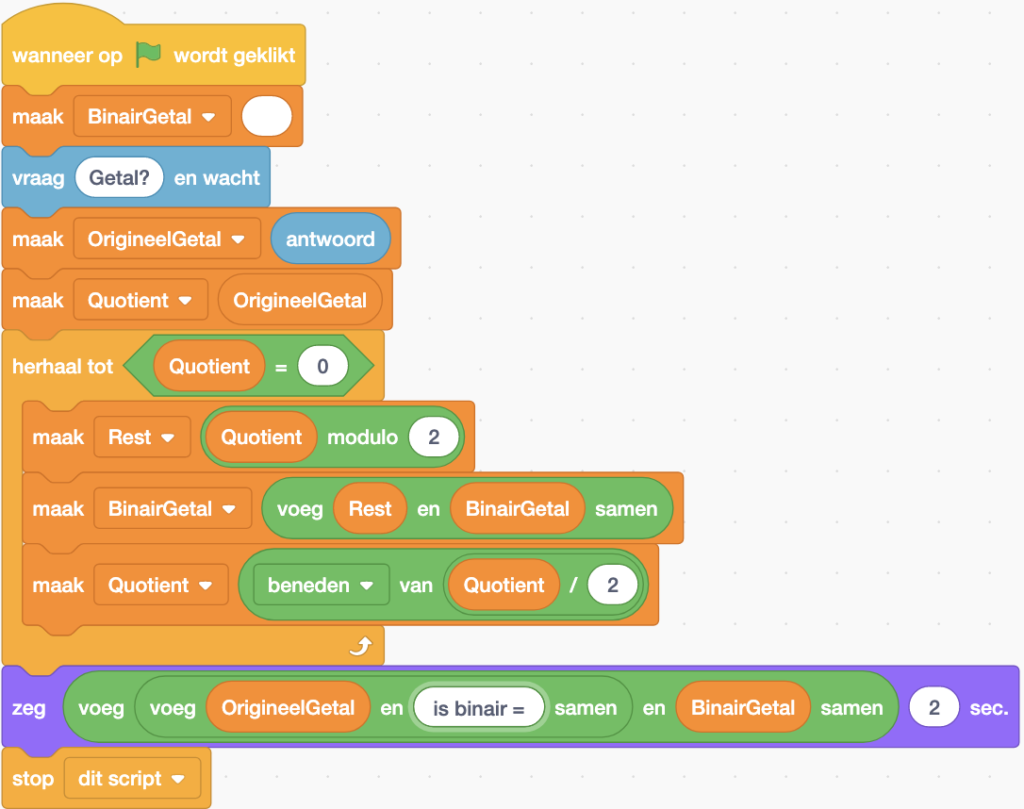
De functie is te vinden in de categorie Functies als onderdeel van de functie . Onder de functie absoluut zijn meerdere andere functies beschikbaar. De functie beneden zal een kommagetal naar beneden afronden naar het dichtstbijzijnde geheel getal (bijvoorbeeld 5 gedeeld door 2 wordt 2.5. De functie beneden rondt het getal 2.5 af naar 2).

De voeg-functies lijken soms wat complex. De voeg-functie plakt steeds twee afzonderlijke gegevens aan elkaar. De instructie plakt de bekomen restwaarde in de variabele Rest aan de voorlopige inhoud van de variabele BinairGetal.

Als we drie elementen willen samenvoegen dan moeten we gebruik maken van twee voeg-functies. Bestudeer even hoe het zeg-blok is samengesteld.