Inleiding
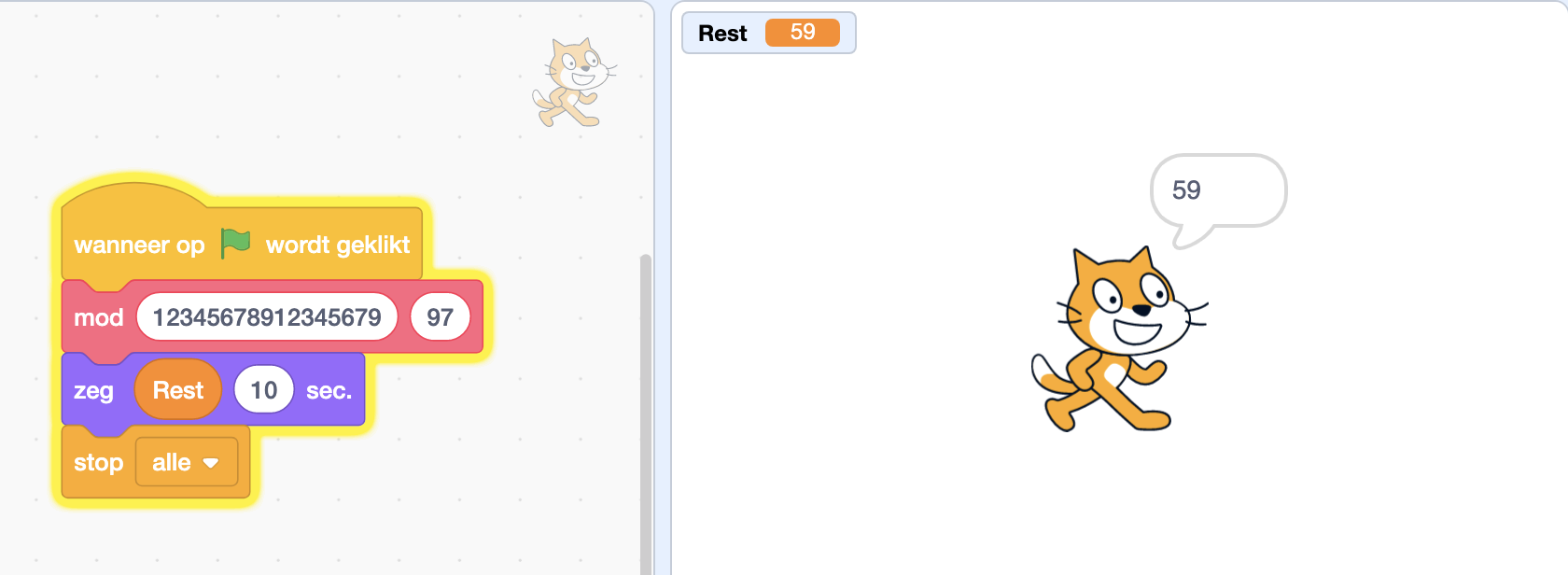
Het hoofdstuk ‘Raar maar Waar’ toont problemen bij het uitvoeren van bewerkingen met heel grote getallen. In alle programmeertalen is de grootte van getallen namelijk beperkt. Dit is ook het geval in Scratch. Bekijk maar even volgende optelling:
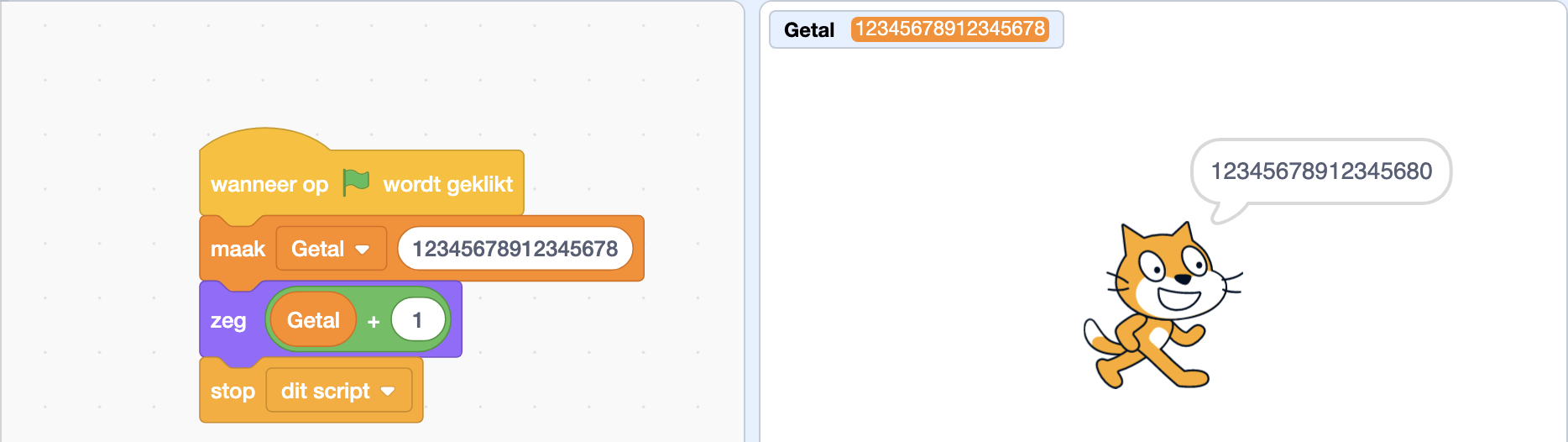
De optelling van 1 bij het getal 12345678912345678 levert de verkeerde waarde 12345678912345680.
De manier waarop heel grote getallen in het interne geheugen worden opgeslagen is de verklaring waarom deze bewerking tot een verkeerd resultaat leidt. Bewerkingen met getallen tot en met 16 cijfers leveren correcte oplossingen. Het resultaat van bewerkingen met getallen bestaande uit meer dan 16 cijfers moeten steeds heel aandachtig worden gecontroleerd.
In het hoofdstuk ‘Raar maar Waar’ zal een oplossing worden gezocht voor het uitvoeren van modulo-bewerkingen met zeer grote getallen.
Modulo-bewerkingen
De modulo-functie laat toe om de rest te berekenen van een deling van twee getallen. Ook deze functie kan tot foutieve resultaten leiden als het deeltal uit meer dan 16 cijfers bestaat. Volgend eenvoudig voorbeeld illustreert het probleem:
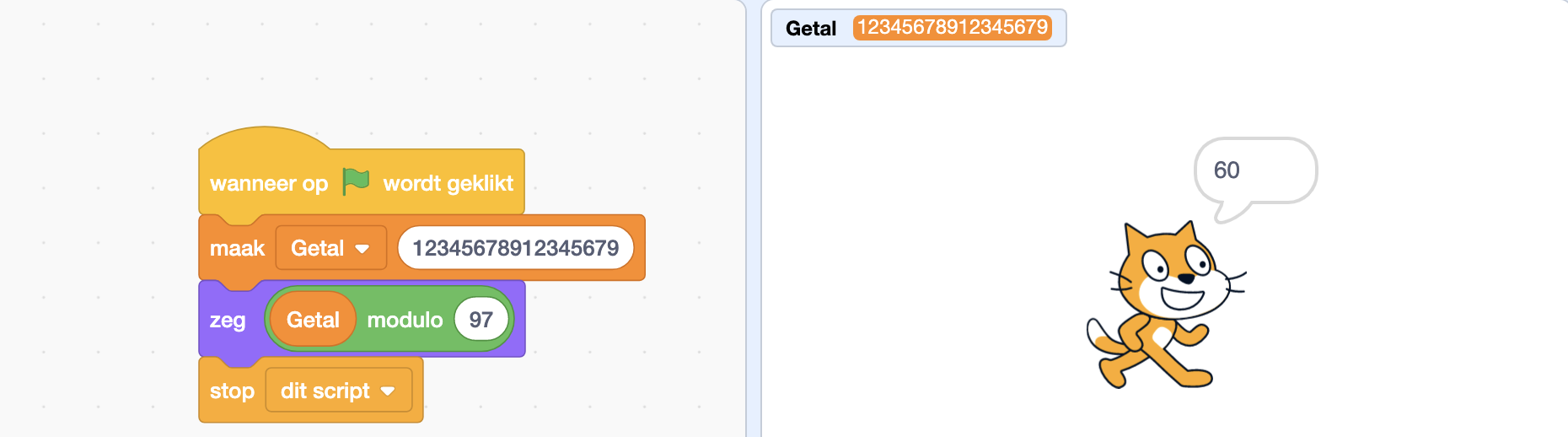
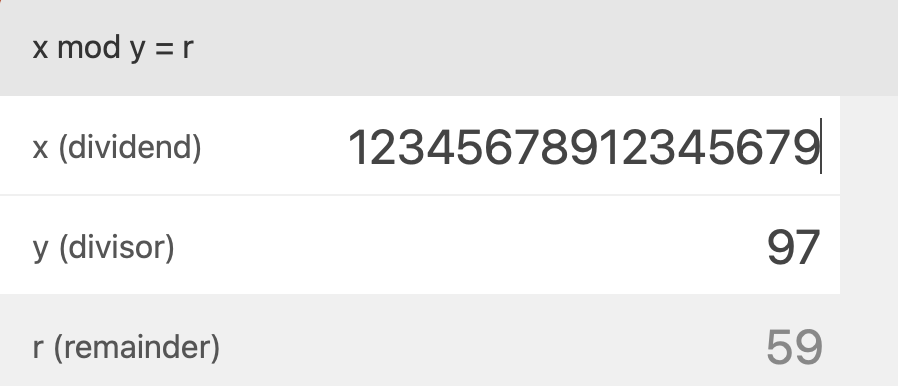
Scratch geeft als rest de waarde 60 voor deze modulo-97-bewerking. Als deze bewerking wordt uitgevoerd via de modulo-app op de website www.omnicalculator.com dan is de restwaarde 59.
Als we toch correcte bewerkingen willen uitvoeren met grote getallen dan moeten we zelf een algoritme ontwikkelen om de bewerking na te bootsen. In dit geval zullen we het grote getal als een string behandelen waarbij het algoritme de string manipuleert om een correcte bewerking uit te voeren.
Algoritme
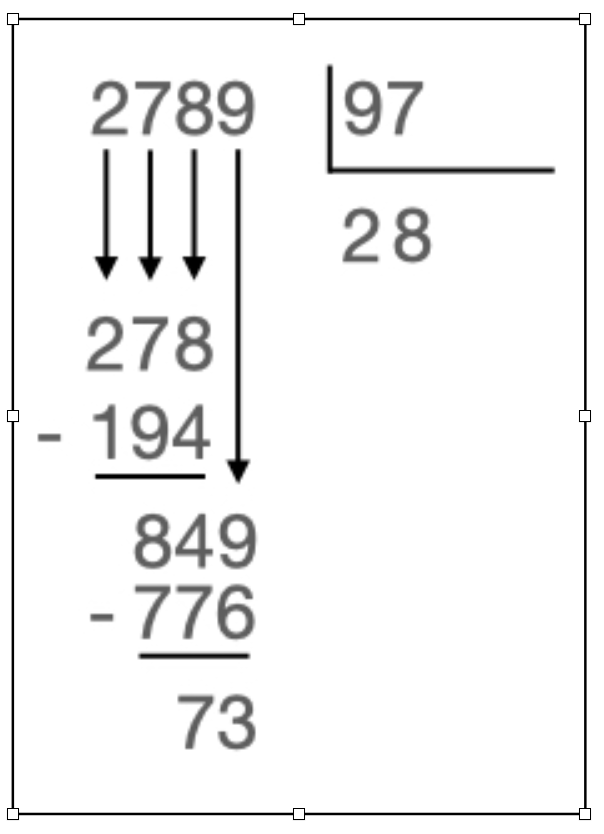
Het algoritme is eigenlijk een nabootsing van de ‘oude’ manier (staartdeling) waarop je een deling uitvoert. Je laat cijfer na cijfer naar beneden vallen waarbij je iedere keer de deling uitvoert en de rest behoudt. Bij het naar beneden brengen van een volgend cijfer wordt de oude restwaarde natuurlijk 10 maal groter (als 7 zakt dan wordt de waarde van de vroegere restwaarde (2) twintig, als 8 zakt dan wordt de waarde van de vroegere restwaarde (27) tweehonderdzeventig,…
In tabelvorm kan de berekening van de restwaarde van 2789 gedeeld door 97 als volgt worden voorgesteld:
| Deeltal (2789) | Deler (97) |
|---|---|
| rest = 0 | |
| rest (0) * 10 + 2 = 2 | 2 : 97 = 0 rest 2 |
| rest (2) * 10 + 7 = 27 | 27 : 97 = 0 rest 27 |
| rest (27) * 10 + 8 = 278 | 278 : 97 = 2 rest 84 |
| rest (84) * 10 + 9 = 849 | 849 : 97 = 8 rest 73 |
Voor de opmaak van de pseudocode gebruiken we volgende variabelen: Deeltal, Deler en Rest. De variabele Positie houdt de plaats bij van het karakter (cijfer) in de string dat wordt behandeld.
De pseudocode kan nu als volgt worden voorgesteld:
Initialiseer Rest op 0
Initialiseer Positie op 1
Repeat voor alle karakters in Deeltal
Maak de variabele Rest gelijk aan de restwaarde van de oude waarde van Rest * 10 aangevuld met het karakter op plaats Positie van Deeltal gedeeld door Deler
Verhoog Positie met 1
End RepeatDe mod-procedure kan nu als volgt in Scratch worden ontwikkeld:
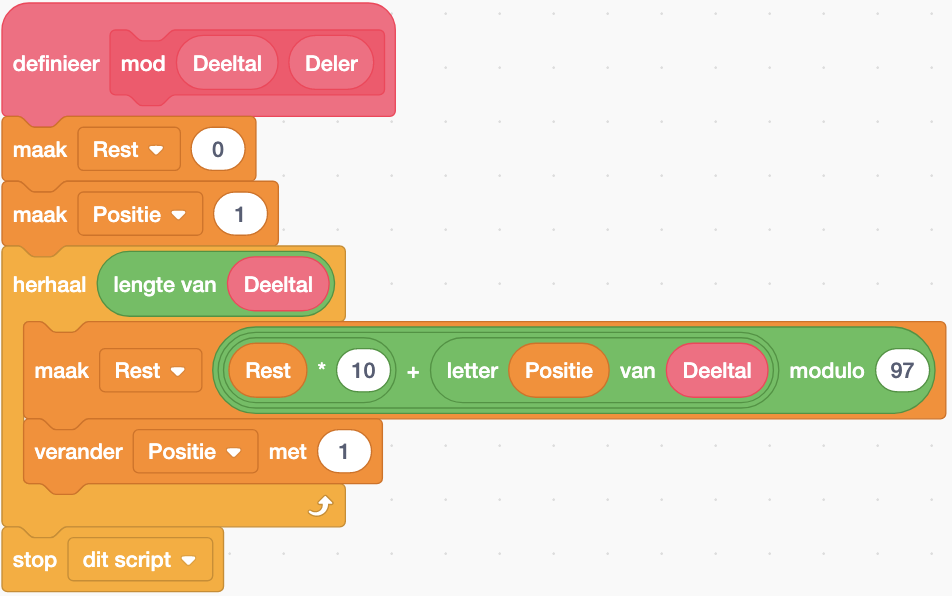
Controleer even of je de ‘complexe’ instructie in het midden van de herhaal– structuur begrijpt. Gebruik hiervoor de tabel met als onderschrift Staartdeling. Bemerk tevens dat we in deze instructie wel de Scratch modulo-functie gebruiken. Het gaat hier namelijk steeds over heel kleine getallen. Scratch heeft geen problemen met berekeningen uitgevoerd met kleine getallen.
Onze mod-procedure leidt nu tot een correcte berekening van de restwaarde van een deling: