Het Beste Algoritme Zoeken

Inleiding

Het is steeds de bedoeling om te zoeken naar het ‘beste’ algoritme om een probleem op te lossen. Hierbij zal je rekening moeten houden met de uitvoeringstijd nodig voor de computer om het resultaat te berekenen, met de complexiteit van het algoritme voor de programmeur en met de leesbaarheid van het programma voor vrienden en collega’s. In dit hoofdstuk illustreren we deze problematiek door drie mogelijke algoritmen te bestuderen om te bepalen of een getal even of oneven is.

Even of Oneven?

Hoe kan een computer bepalen of een willekeurig getal, ingebracht door een gebruiker, even of oneven is? Dit lijkt een eenvoudig probleem maar steeds krijg je de meest diverse oplossingen voorgeschoteld. In volgende paragrafen bestuderen we enkele mogelijke algoritmen.

Algoritme 1: 0 = Even, 1 = Oneven

In dit algoritme wordt voorgesteld om meerdere malen het getal 2 af te trekken van het oorspronkelijk getal tot de waarde 0 of 1 wordt bereikt. Als de eindwaarde 0 is dan was het oorspronkelijk getal even, als de eindwaarde 1 is dan was het oorspronkelijk getal oneven.

Pseudocode

Deze logica kan gemakkelijk in pseudocode worden omgezet:

Input Getal
Repeat Until Getal = 0 OR Getal = 1
   Getal = Getal - 2
End Repeat
If Getal = 0 Then
   Output "Het getal is even"
Else
   Output "Het getal is oneven"
End If

De voorwaarde vermeld in de Repeat Until vraagt wat meer uitleg. De Repeat Until duidt aan wanneer de uitvoering van de lus moet stoppen. In dit geval stopt de uitvoering van de herhaling wanneer de variabele Getal de waarde 0 of (OR) de waarde 1 heeft bereikt. Eén van beide voorwaarden is voldoende om de Repeat Until te beëindigen.

De instructie Getal = Getal – 2 lijkt wat eigenaardig. Hoe kan het linkerlid gelijk zijn aan het rechterlid? Dit is evenwel een traditionele schrijfwijze om aan te duiden dat het resultaat van de bewerking vermeld rechts van het =-teken wordt opgeslagen in de variabele links van het =-teken. Dus eerst wordt de variabele Getal met 2 verminderd en daarna wordt het resultaat van deze bewerking terug gestockeerd in de variabele Getal. Het =-teken is dus niet een gelijkheidsteken maar een toewijzingsteken (we wijzen het resultaat van de bewerking in het rechterlid toe aan de variabele in het linkerlid).

Scratch-Programma

Zoals je al weet zijn voorwaarden beschikbaar in de categorie Functies. De ‘complexe’ voorwaarde van de Repeat Until wordt in drie stappen opgebouwd: de eerste voorwaarde , daarna de tweede voorwaarde en uiteindelijk worden beide voorwaarden toegevoegd aan de of-functie .

Het volledig Scratch-programma ziet er dan als volgt uit:

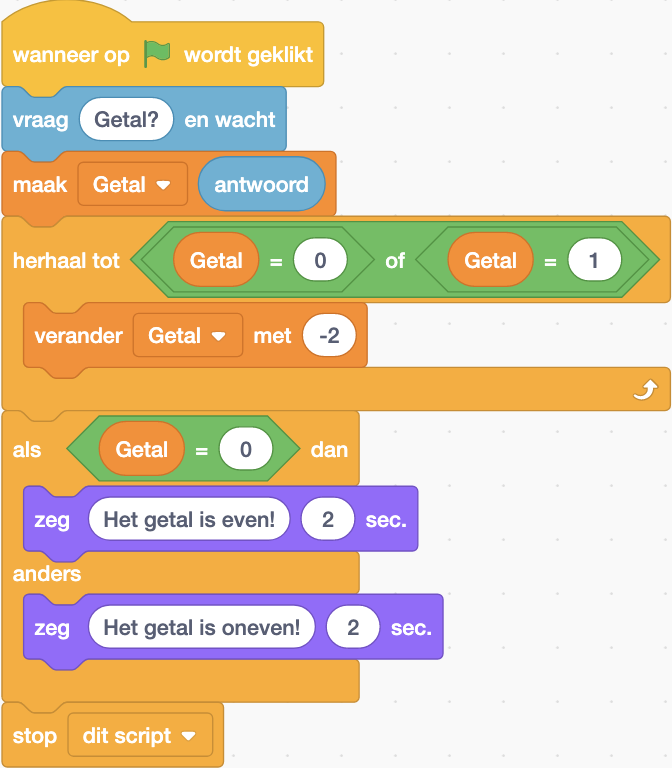
Dit programma lijkt prima te werken. Toch zijn er een aantal bemerkingen te formuleren:

1. De oorspronkelijke waarde van de variabele Getal is op het einde van het programma niet meer beschikbaar (de variabele Getal zal namelijk op het einde van het programma ofwel 0 ofwel 1 zijn). Hoe kan je ervoor zorgen dat de oorspronkelijke waarde ook nog bewaard blijft?
2. Werkt het programma ook voor negatieve getallen? Wat doet het programma als je een negatief getal inbrengt? Hoe kan je dit probleem oplossen?
3. Breng eens een heel groot positief getal in (bijvoorbeeld 1876543218). Het zal je wel opvallen hoelang de computer nodig heeft om te bepalen of dit getal even of oneven is. Dit programma is dus wel correct maar is niet erg goed bruikbaar voor grote getallen.

Algoritme 2: Deling door 2

Een ander algoritme zou kunnen zijn om het oorspronkelijk getal door 2 te delen. Indien de deling een geheel getal oplevert dan is het oorspronkelijk getal even, indien de deling een decimaal getal oplevert dan is het oorspronkelijk getal oneven.

Pseudocode

Input Getal
Getal = Getal / 2
If Getal = geheel getal Then
   Output "Het getal is even"
Else
   Output "Het getal is oneven"
End If

Scratch-Programma

Dit lijkt heel erg eenvoudig. De vraag is natuurlijk: welke instructie hebben we in Scratch ter beschikking om te controleren of het resultaat van de deling een geheel getal is?

De functie afgerond (te vinden in de categorie Functies) biedt op deze vraag een gemakkelijke oplossing. De functie afgerond zal een getal afronden naar het dichtstbijzijnde geheel getal: afgerond(1.4) wordt 1, afgerond(1.6) wordt 2, afgerond(1.5) wordt ook 2. Indien de niet-afgeronde versie van het resultaat van de deling nu gelijk is aan de afgeronde versie van het resultaat dan was het oorspronkelijk getal natuurlijk even.

Het volledig programma ziet er nu als volgt uit:

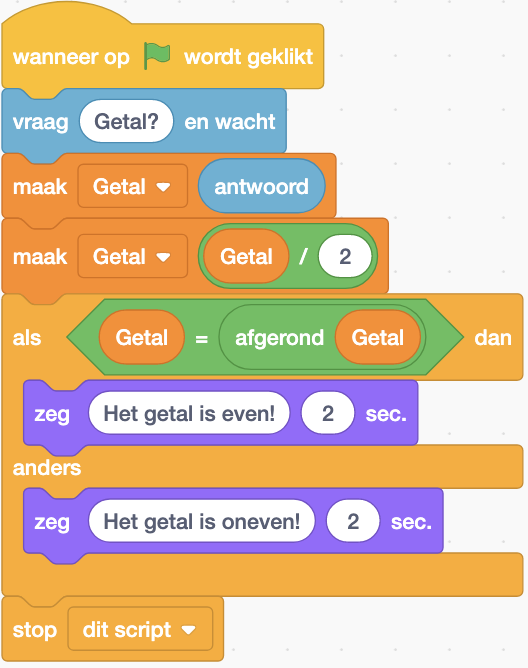
De als…dan…anders…-structuur is gemakkelijk te begrijpen vanuit een voorbeeld: als het oorspronkelijk getal 17 was dan bevat de variabele Getal na de deling door 2 de waarde 8.5. De functie afgerond(8.5) levert dan de waarde 9. Als we dan 8.5 op gelijkheid controleren met 9 dan is de vergelijking onwaar (False) en dus is het oorspronkelijk getal oneven.

Dit programma is zeker heel wat beter dan de vorige versie van ons algoritme. De uitvoeringstijd van het algoritme is, zelfs voor heel grote getallen, steeds dezelfde. Tevens kan dit programma ook negatieve getallen correct beoordelen.

Ook in dit geval is het oorspronkelijk getal natuurlijk vernietigd. Pas het programma nu even aan om het oorspronkelijk getal beschikbaar te houden aan het einde van het programma.

Algoritme 3: Modulo

De functie modulo geeft als resultaat de restwaarde van een deling door een bepaald getal. Als we vorig voorbeeld opnieuw gebruiken dan is de restwaarde van 17 gedeeld door 2 gelijk aan 1 (17 modulo 2). Als de restwaarde 1 is dan is het getal natuurlijk oneven. Het gebruik van deze eenvoudige functie maakt ons programma heel goed leesbaar en begrijpbaar.

Pseudocode

Input Getal
Getal = Getal modulo 2
If Getal = 0 Then
  Output "Het getal is even"
Else
   Output "Het getal is oneven"
End If

Scratch-Programma

De functie modulo is te vinden in de categorie Functies . Het volledig programma ziet er dan als volgt uit:

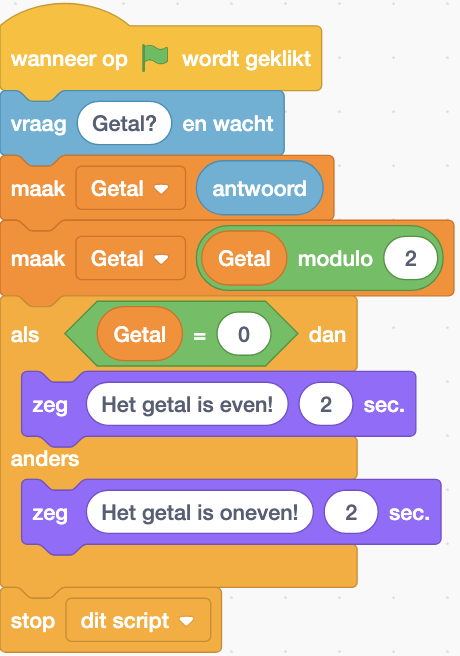
Het oorspronkelijk getal is natuurlijk ook weer vernietigd. Pas dit programma aan zodat het getal nog steeds beschikbaar is aan het einde van het programma.

Eindevaluatie

De drie algoritmen leiden tot een correct resultaat. Het eerste algoritme is niet aanvaardbaar omwille van de benodigde uitvoeringstijd voor grote getallen. Het tweede algoritme is aanvaardbaar maar vereist wat studiewerk om de ‘moeilijke’ als…dan…anders…-structuur te begrijpen. Het derde algoritme is snel, eenvoudig en leesbaar en verdient dan ook onze voorkeur.