Van Binair naar Decimaal

Inleiding

In de les Van Binair naar Decimaal wordt een programma ontwikkeld om een binair getal te converteren naar een decimaal getal (tiendelig stelsel).

Van Binair naar Decimaal: Algoritme

Hoe een binair getal omzetten naar een decimaal getal?

Vanuit vorig hoofdstuk weten we dat de plaats van een bit in een binair patroon bepaalt wat de waarde is die met deze plaats overeenkomt. We beginnen steeds van rechts naar links. De meest rechtse plaats vermenigvuldigt de waarde van de bit met 2⁰ (=1), de voorlaatste plaats vermenigvuldigt de waarde van de bit met 2¹ (=2), de daaropvolgende plaats vermenigvuldigt de waarde van de bit met 2² (=4)… Elke plaats neemt dus de waarde van de voorgaande plaats en vermenigvuldigt deze waarde met 2. Dus 1, 2, 4, 8, 16, 32, 64, 128, 256… Volgend voorbeeld kan de berekening verduidelijken:

De laatste plaats van het binair getal wordt steeds vermenigvuldigd met 1, de voorlaatste plaats met 2 (voorgaande waarde 1 * 2), de voorgaande plaats met 4 (voorgaande waarde 2 * 2), de eerste bit met 8 (voorgaande waarde 4 * 2).

Variabelen

De eerste variabele is in ieder geval het binair getal dat we wensen te converteren. We kunnen deze variabele BinairGetal noemen. De plaats van de bit in het binair getal (genummerd 1, 2, 3, 4… van links naar rechts) kunnen we aanduiden met de variabele Positie en de waarde van een bit op een welbepaalde positie (de laatste, meest rechtse bit krijgt de waarde 1, de voorgaande bit krijgt de waarde 2, daarna 4, daarna 8…) kunnen we aangeven in de variabele PositieWaarde. De actuele PositieWaarde is steeds de voorgaande PositieWaarde vermenigvuldigt met 2. Het decimaal getal (variabele DecimaalGetal) wordt stapsgewijs opgebouwd.

Pseudocode

Input BinairGetal
Plaats DecimaalGetal op 0
Plaats het aantal bits van de variabele BinairGetal in Positie
Plaats PositieWaarde op 1
Repeat Until Positie = 0
   Vervang DecimaalGetal door DecimaalGetal + bit op plaats Positie *  PositieWaarde
   Plaats PositieWaarde op PositieWaarde * 2
   Verminder Positie met 1
End Repeat
Output DecimaalGetal

Als we alle bits in BinairGetal afzonderlijk nummeren dan is de meest linkse bit de eerste bit in de reeks. Bij de start laten we de variabele Positie verwijzen naar de laatste bit (meest rechtse) in de reeks. In voorgaand voorbeeld is dit bit met nummer 4. De berekening is dan de waarde van de bit op de vierde positie (1) vermenigvuldigd met de PositieWaarde die gelijk is aan 1. Daarna wordt de PositieWaarde met 2 vermenigvuldigd om te verwijzen naar de waarde van een bit op de derde positie van de reeks. De variabele Positie wordt natuurlijk ook met 1 verminderd en wordt dan 3. De lus stopt als er geen te onderzoeken bits meer overblijven (als de variabele Positie gelijk is aan 0).

In volgende tabel wordt de werking van het algoritme voor het BinairGetal 1101 nog even nagebootst:

Positie	Bit	PositieWaarde	DecimaalGetal
4	1	1	0 + 1 * 1 = 1
3	0	1 * 2 = 2	1 + 0 * 2 = 1
2	1	2 * 2 = 4	1 + 1 * 4 = 5
1	1	4 * 2 + 8	5 + 1 * 8 = 13

Van Binair naar Decimaal: Scratch-programma

Het Scratch-programma kan nu als volgt worden opgebouwd:

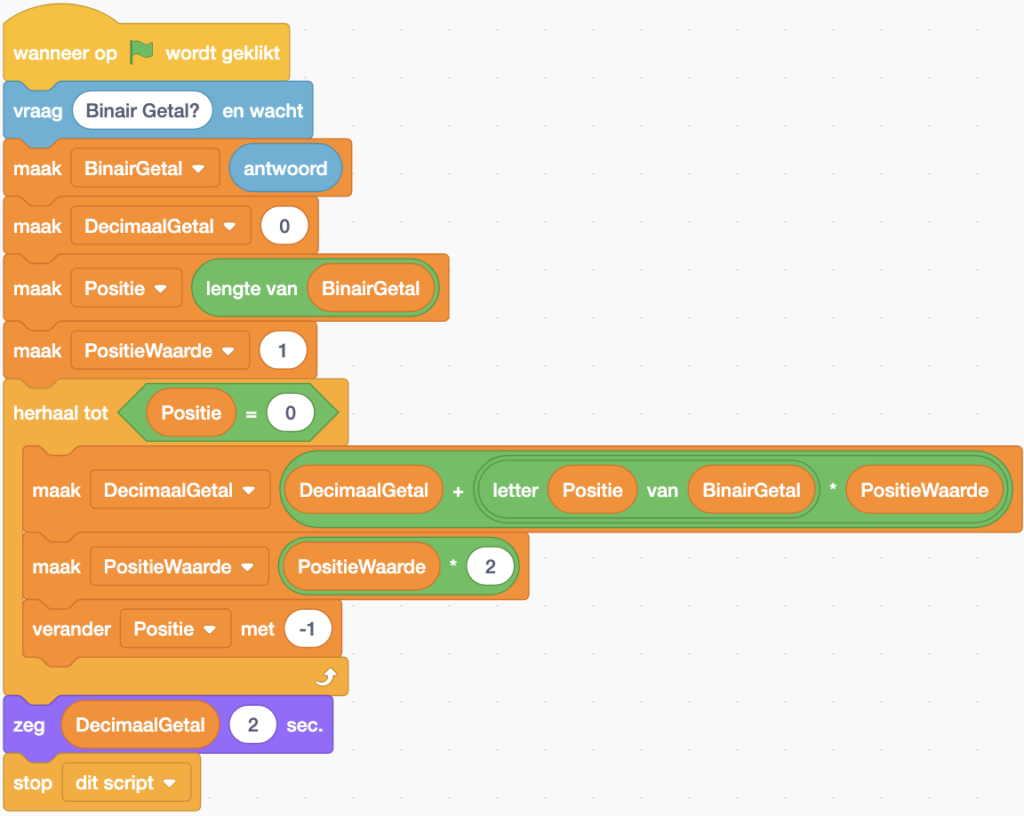
Het blok gebruikt de functie (categorie Functies) om te bepalen uit hoeveel karakters een tekst bestaat. De lengte (4 in bovenstaand voorbeeld) wordt door het maak-blok geplaatst in de variabele Positie.

Het blok gebruikt de functie (categorie Functies) om één bepaalde letter op te halen uit een bepaalde tekst. In bovenstaand maak-blok wordt het karakter aangeduid door de variabele Positie opgehaald uit de variabele BinairGetal en vermenigvuldigd met de PositieWaarde. Deze berekening wordt dan opgeteld bij de voorlopige waarde van de variabele DecimaalGetal. De werking wordt geïllustreerd in de tabel Simulatie van de pseudocode.